Maximum Cut

A maximum cut of a graph is a partition of its vertices into two sets, \(S\) and \(T\), such that the number of edges between them is maximized. The task of finding such a cut is known as the MaxCut Problem.

The Cost Function

Given a graph \(G=(V, E)\), the cost function to minimize for the MaxCut problem is given by

\[ C(\textbf{x}) = -\sum_{(i, j)\in E} w_{ij} (x_i+x_j - 2x_i x_j ) \]

where \(w_{ij}\) is the weight corresponding to the edge \((i,j) \in E\), and \(\textbf{x}\in \{0, 1\}^{|V|}\) is the binary variable indicating whether node \(i\) is in set \(S\) or \(T\). This works because each term \(x_i+x_j - 2x_i x_j\) is equal to 1 if an edge is in the cut, and 0 otherwise.

Note that the equivalent formulation in terms of Ising variables is the following

\[ C(\sigma) = -\sum_{(i, j)\in E} w_{ij} \sigma_i\sigma_j, \]

where this time \(\sigma \in \{-1, 1\}^{|V|}\).

MaxCut in OpenQAOA

MaxCut being a graph problem, you can leverage the popular networkx to easily create a variety of graphs. For example, an Erdös-Rényi graph can be instantiated with

import networkx as nx

G = nx.generators.fast_gnp_random_graph(n=6, p=0.6, seed=42)

OpenQAOA has a nice wrapper to plot networkx graphs

from openqaoa.utilities import plot_graph
plot_graph(G)

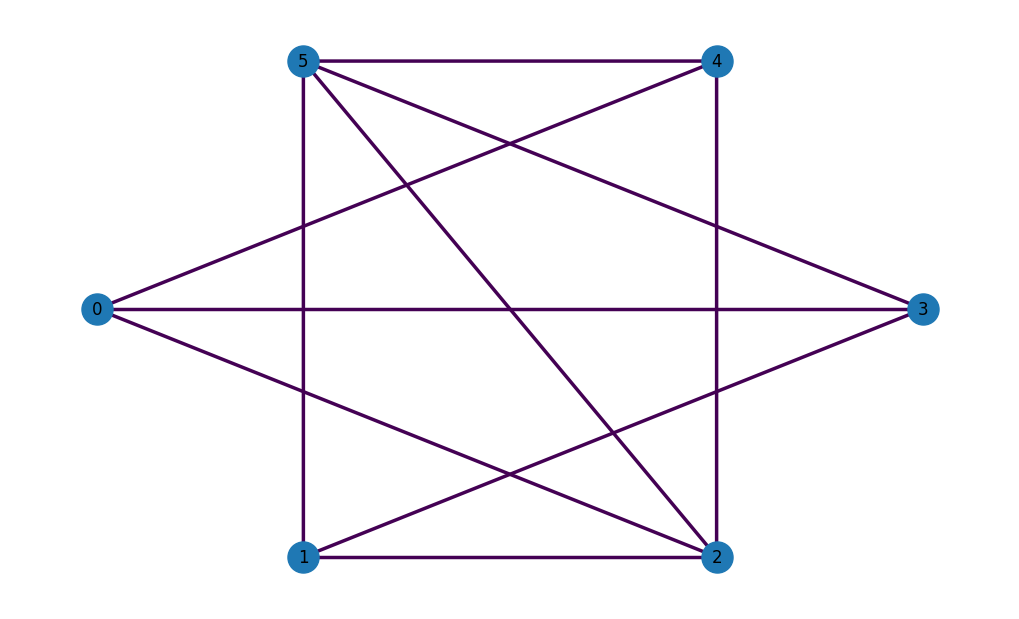
Once the graph is defined, creating a MaxCut problem class requires only a few lines of code:

from openqaoa.problems import MaximumCut

maxcut_prob = MaximumCut(G)
maxcut_qubo = maxcut_prob.qubo

We can then access the underlying cost hamiltonian

maxcut_qubo.hamiltonian.expression

\[ 1.0Z_{0}Z_{2} + 1.0Z_{0}Z_{3} + 1.0Z_{0}Z_{4} + 1.0Z_{1}Z_{2} + 1.0Z_{1}Z_{3} + 1.0Z_{1}Z_{5} + 1.0Z_{2}Z_{4} + 1.0Z_{2}Z_{5} + 1.0Z_{3}Z_{5} + 1.0Z_{4}Z_{5} \]

You may also check all details of the problem instance in the form of a dictionary:

> maxcut_qubo.asdict()

{'constant': 0,
'metadata': {},
'n': 6,
'problem_instance': {'G': {'directed': False,
                            'graph': {},
                            'links': [{'source': 0, 'target': 2},
                                    {'source': 0, 'target': 3},
                                    {'source': 0, 'target': 4},
                                    {'source': 1, 'target': 2},
                                    {'source': 1, 'target': 3},
                                    {'source': 1, 'target': 5},
                                    {'source': 2, 'target': 4},
                                    {'source': 2, 'target': 5},
                                    {'source': 3, 'target': 5},
                                    {'source': 4, 'target': 5}],
                            'multigraph': False,
                            'nodes': [{'id': 0},
                                    {'id': 1},
                                    {'id': 2},
                                    {'id': 3},
                                    {'id': 4},
                                    {'id': 5}]},
                    'problem_type': 'maximum_cut'},
'terms': [[0, 2],
        [0, 3],
        [0, 4],
        [1, 2],
        [1, 3],
        [1, 5],
        [2, 4],
        [2, 5],
        [3, 5],
        [4, 5]],
'weights': [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]}