Minimum Vertex Cover

The Minimum Vertex Cover (MVC) problem is a common constrained optimization problem. Given a graph \(G=(V, E)\), the goal is to find a set of vertices \(S \subseteq V\) of minimum cardinality with the constraint that it "covers" all edges in \(G\). For a given \(S\), an edge \((i, j) \in E\) is said to be covered if at least one of its constituent vertices is part of \(S\).

The Cost Function

The corresponding function to minimize can be derived as:

\[ C(\textbf{x}) = \sum_{i \in V}x_i + P\sum_{(i, j) \in E}\left(1-x_i\right)\left(1-x_j\right), \]

where \(\textbf{x}\in \{0, 1\}^{|V|}\) and \(P>1\) is the penalty, a parameter controlling the strength of penalization of configurations which are not covers.

Interpreting a variable \(x_i\) being equal to 1 as being part of the vertex cover, the first summation counts the size of the selected cover while the second summation ensures that the selected cover indeed covers all edges. Hence, minimizing it ensures we find the minimum vertex cover.

Note that this cost function can be conveniently converted to the form of an Ising problem in order to be usable with QAOA (see what-is-a-qubo).

Minimum Vertex Cover in OpenQAOA

MVC being a graph problem, you can leverage the popular networkx to easily create a variety of graphs. For example, an Erdös-Rényi graph can be instantiated with

import networkx as nx

G = nx.generators.fast_gnp_random_graph(n=6, p=0.6, seed=42)

OpenQAOA has a nice wrapper to plot networkx graphs

from openqaoa.utilities import plot_graph
plot_graph(G)

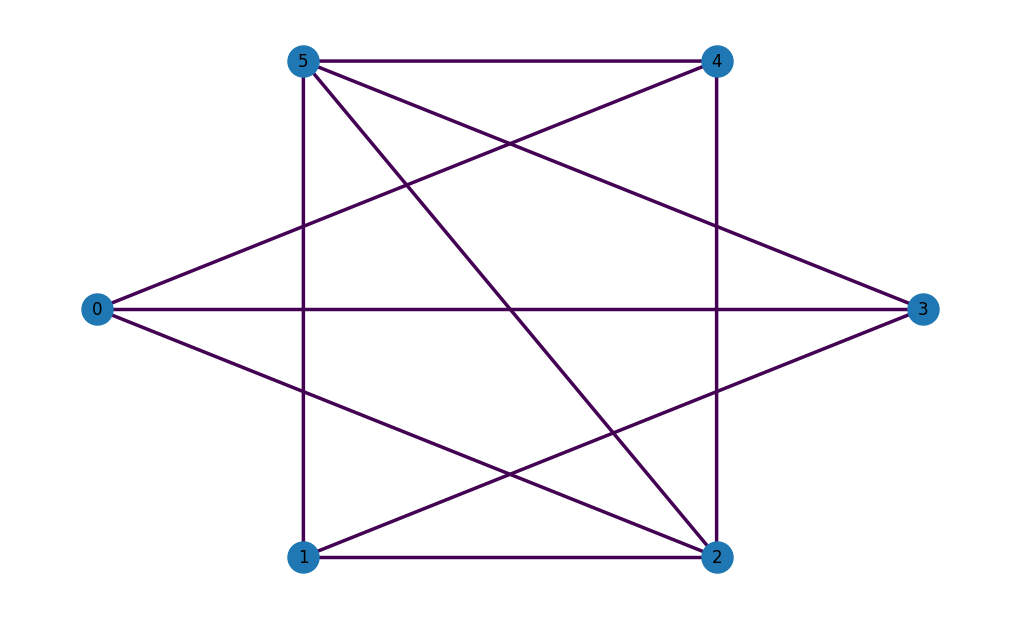
Once the graph is defined, creating a MVC problem class requires only a few lines of code, including the graph as well as two extra parameters, field and penalty:

from openqaoa.problems import MinimumVertexCover

mvc_prob = MinimumVertexCover(G, field=1.0, penalty=10)
mvc_qubo = mvc_prob.qubo

We can then access the underlying cost hamiltonian

mvc_qubo.hamiltonian.expression

\[ 2.5Z_{0}Z_{2} + 2.5Z_{0}Z_{3} + 2.5Z_{0}Z_{4} + 2.5Z_{1}Z_{2} + 2.5Z_{1}Z_{3} + 2.5Z_{1}Z_{5} + 2.5Z_{2}Z_{4} + 2.5Z_{2}Z_{5} + 2.5Z_{3}Z_{5} + 2.5Z_{4}Z_{5} + 28.0 + 7.0Z_{0} + 7.0Z_{1} + 7.0Z_{3} + 7.0Z_{4} + 9.5Z_{2} + 9.5Z_{5} \]

You may also check all details of the problem instance in the form of a dictionary:

> mvc_qubo.asdict()

{'constant': 28.0,
 'metadata': {},
 'n': 6,
 'problem_instance': {'G': {'directed': False,
                            'graph': {},
                            'links': [{'source': 0, 'target': 2},
                                      {'source': 0, 'target': 3},
                                      {'source': 0, 'target': 4},
                                      {'source': 1, 'target': 2},
                                      {'source': 1, 'target': 3},
                                      {'source': 1, 'target': 5},
                                      {'source': 2, 'target': 4},
                                      {'source': 2, 'target': 5},
                                      {'source': 3, 'target': 5},
                                      {'source': 4, 'target': 5}],
                            'multigraph': False,
                            'nodes': [{'id': 0},
                                      {'id': 1},
                                      {'id': 2},
                                      {'id': 3},
                                      {'id': 4},
                                      {'id': 5}]},
                      'field': 1.0,
                      'penalty': 10,
                      'problem_type': 'minimum_vertex_cover'},
 'terms': [[0, 2],
           [0, 3],
           [0, 4],
           [1, 2],
           [1, 3],
           [1, 5],
           [2, 4],
           [2, 5],
           [3, 5],
           [4, 5],
           [0],
           [1],
           [2],
           [3],
           [4],
           [5]],
 'weights': [2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 7.0, 7.0, 9.5, 7.0, 7.0, 9.5]}